In the previous lecture, we learnt the theory behind precise calibration of photometry, enabling us to put photometric observations onto a standard scale with precisions of better than 1%. In this practical we are going to learn how to produce calibrated photometry using a simplified method. This method does not yield the same accuracy as an analysis using observations of primary or secondary standard stars, combined with the use of colour terms. On the other hand, it is much simpler to apply, and even works to produce calibrated photometry through thin cloud. If you are happy to accept accuracies on the order of a few percent, I recommend using the method described below whenever you need to produce calibrated photometry.
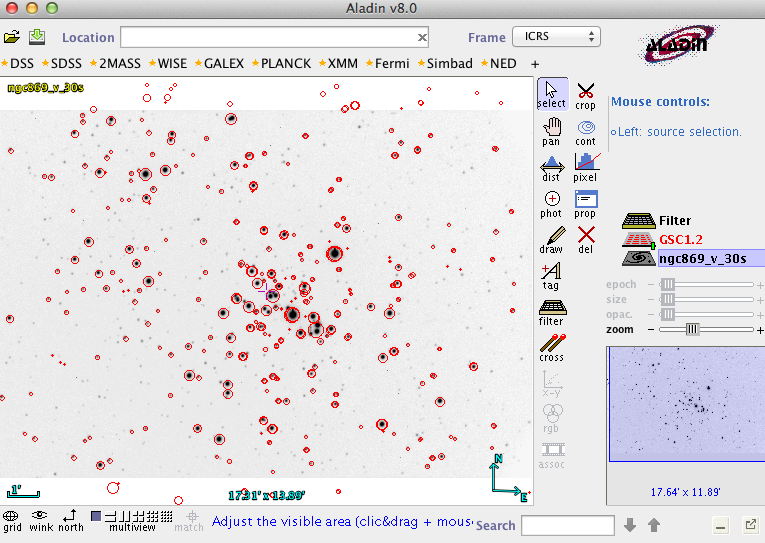
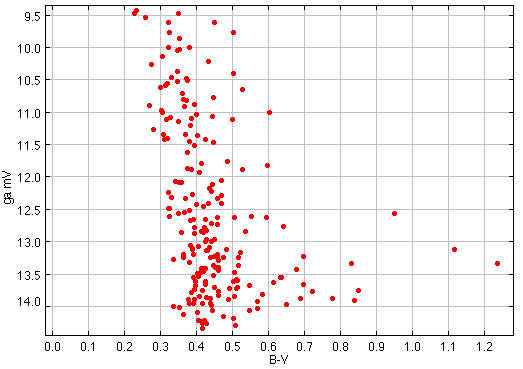
In this practical, we will produce a colour-magnitude diagram of the young open cluster NGC 869, using readily available software. First, I describe the method which will enable us to obtain calibrated magnitudes.
Method
In the last lecture we saw that, for any star, the difference between the calibrated magnitude, \(m\) and the above-atmosphere instrumental magnitude \(m_{0,i}\) is given by: \[m = m_{0,i} + m_{\rm zp},\] where \(m_{\rm zp}\) is known as the zero point. The above-atmosphere instrumental magnitude is given by: \[m_{0,i} = m_i - kX,\] where \(m_i = -2.5 \log_{10} \left( N_t/t_{\rm exp} \right)\) is the instrumental magnitude, \(k\) is the extinction coefficient, and \(X\) is the airmass. Therefore: \[m = m_i - kX + m_{\rm zp}.\] In other words, if we were to plot the calibrated magnitude \(m\) against instrumental magnitude \(m_i\) for all the stars in our image, we would expect a straight line, with a gradient of one, and an intercept equal to \( kX + m_{\rm zp} \). This intercept could then be added to all of our instrumental magnitudes to produce calibrated magnitudes.
What makes this technique possible, is the existence of large sky surveys, which have provided calibrated magnitudes for many, relatively bright stars over a very wide areas of the sky. If your data is covered by one of these surveys, and it provides calibrated magnitudes in the same filter as your data, you can apply this technique relatively quickly.
Accuracy
The accuracy this technique can achieve is limited by two factors. First of all we are not taking into account any secondary effects, such as 2nd-order extinction, or colour terms. Secondly, our photometry cannot be any more accurate than that in the sky survey we use. Typically, large sky surveys achieve accuracies of a few percent. Ignoring the secondary effects will probably introduce errors on a similar level. If you need calibrated photometry to better than a few percent, you will have to observe standard stars, and apply the rigorous method described in the previous lecture.
Steps
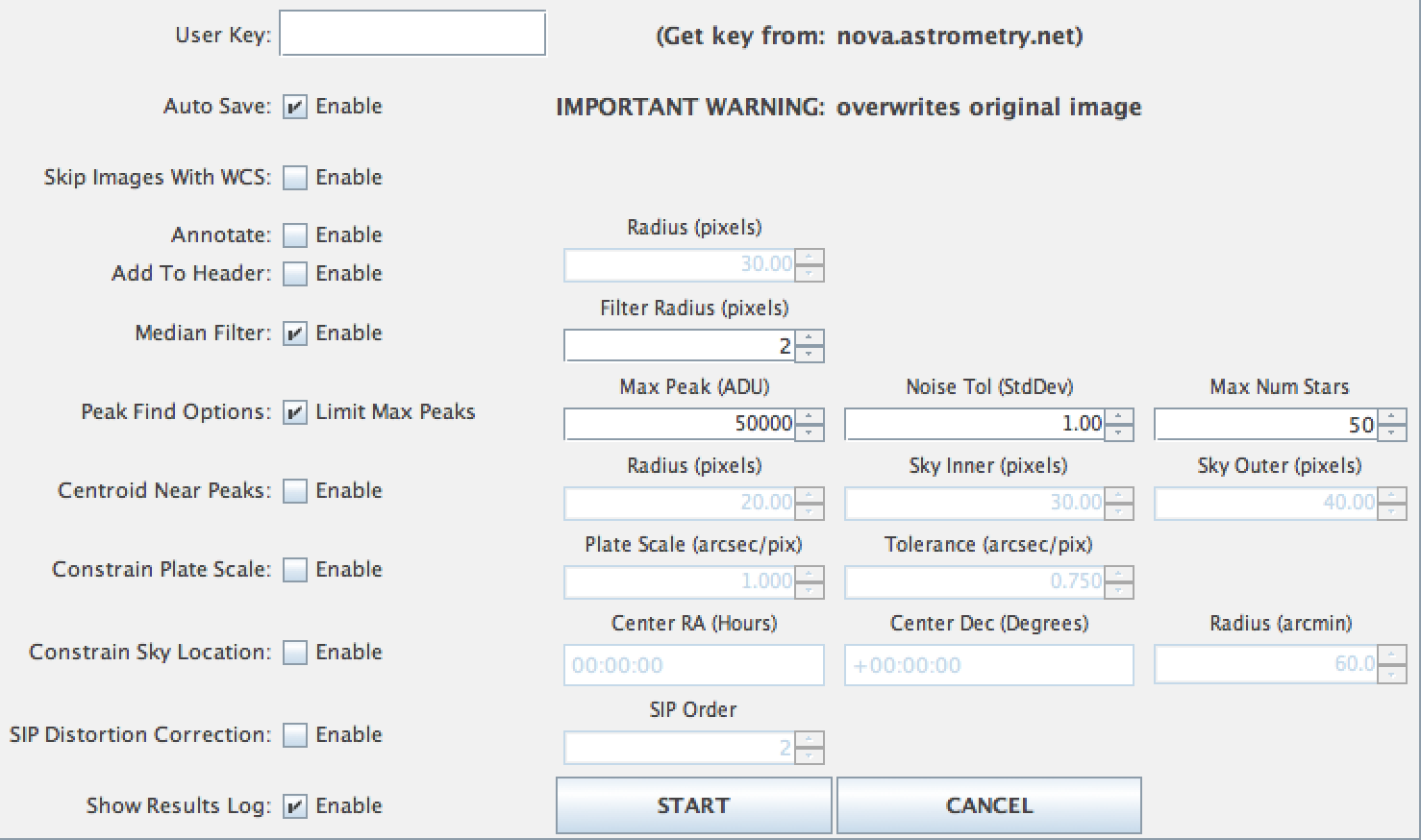
Applying this method requires the application of four steps. These steps are:
- astrometric solution of the image - so we know the RA and Dec of all the stars we measure in our image;
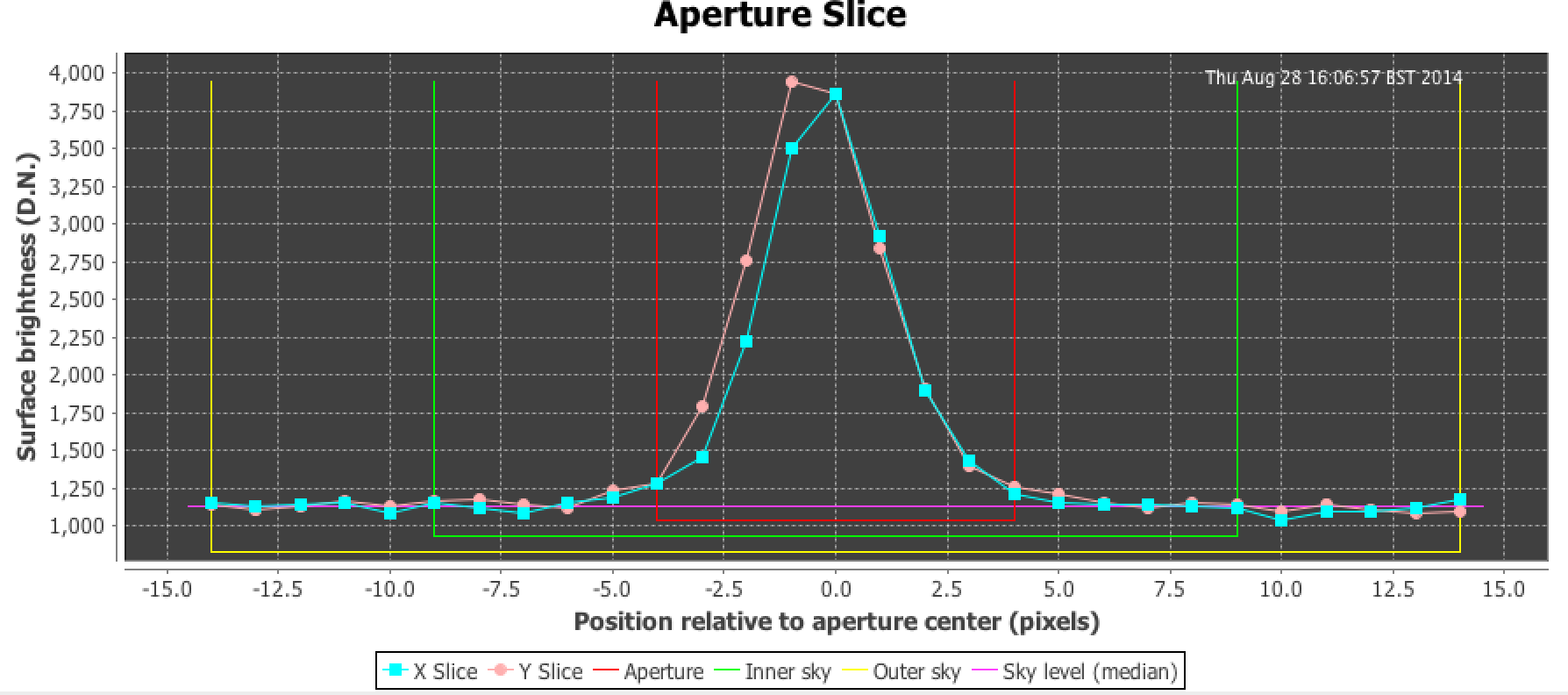
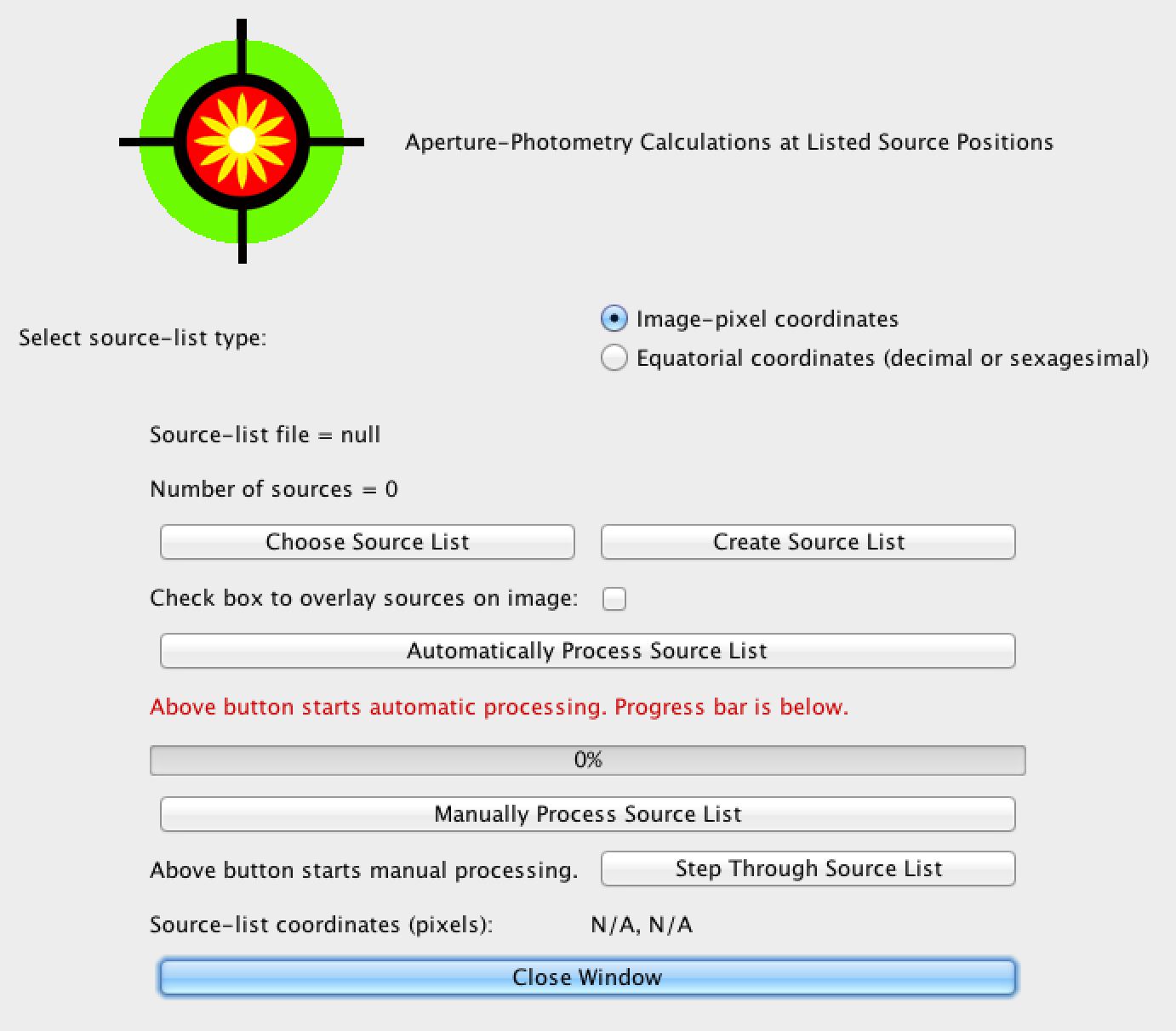
- finding the stars in our image, and calculating instrumental magnitudes;
- matching our stars against a sky-survey, so we know instrumental and calibrated magnitude for many stars;
- calculating the offset between instrumental and calibrated magnitudes, and applying to all stars in our image.
We will need to use several software packages to perform these steps and achieve our goal. Following the guide below will show you how to achieve this with readily available, cross-platform software packages.
The Data
You will need a copy of the data. The data files are located at C:\SharedFolder\astrolab\NGC869\Images.
You don't need to copy the data from this location to work on it, but this folder is local to the PC you are working on now. If you want to save these files for later, you will need to copy them to your M: or U: drives.