In the previous lectures we have seen how light arrives at our telescopes, but how do telescopes work to create an image? In the next block of lectures we're going to look at telescopes - how they work, and the pros and cons of different telescope designs. Telescopes are vital to astronomy, as they fulfil two roles:

1. they allow the collection of light over a much larger area, so that faint objects can be studied,
2. they provide higher angular resolution, allowing studies in greater spatial detail.

All telescope designs share certain basic principles of operations. We start with those principles.

Basic Principles

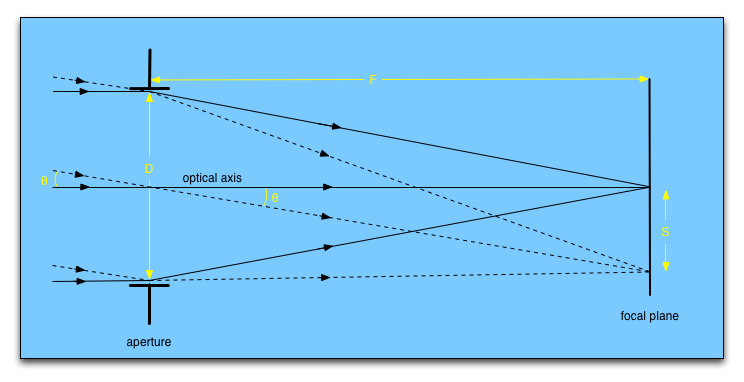
Figure 34 shows a schematic of a telescope. On the left, light from two distant sources arrives at the telescope. As all astronomical sources are effectively at an infinite distance compared to the dimensions of a telescope, the rays from each source can be assumed to be parallel.

The light is collected by an aperture of diameter \(D\) which forms an image of the two sources at the focal plane. The line through the centre of the aperture and the focal plane, and orthogonal to them, defines the optical axis of the system. Since the sources are at infinity, the focal length, \(F\), of the telescope is defined by the distance between the focal plane and the aperture. In astronomical telescopes, the aperture is usually a lens or a mirror, and is circular, hence the amount of light collected is proportional to \(D^2\).

The aperture diameter is the single most important parameter affecting the performance of a telescope and hence most telescopes are usually referred to in terms of it, e.g. the ESO 3.6m telescope in Chile, where the 3.6m is the diameter of its primary mirror.

From figure 34, we can define two terms which are important for describing the specifications of a telescope.

Platescale

The plate scale, \(p\) relates the size of the image in the focal plane, \(s\), to it's angular size on the sky, \(\theta\). Given that \(\theta\) is usually small, we can apply the small angle approximation. Figure 34 shows that \(s\) and \(\theta\) are related by: \[ s=F \theta, \] where \(\theta\) is measured in radians. If we want to study an object with angular size \(\theta\) in high spatial detail, then \(s\) needs to be large. Therefore \(F\) needs to be large; we require a telescope with a long focal length.

The plate scale is the ratio between the angular size and the image size. In other words, \(p = \theta / s \). Since \(s=F \theta\), it follows that \(p = 1/F. \) Since we have used the small angle approximation, if \(F\) is measured in mm, this is the plate scale in radians per mm. It is more usual to quote the plate scale in arc seconds per mm. Since there is 206265 arc seconds in one radian, the plate scale in arc seconds per mm is given by \[p = 206265/F,\] where \(F\) is measured in mm.

Focal ratio

The focal ratio \(f\) is defined as the ratio of the focal length to the diameter, i.e \(f = F/D\). The focal ratio is often used to describe the speed of a telescope (it is used in photography the same way). this can be understood as follows. If we fix \(F\), the image scale \(s\) remains the same. For a smaller \(D\), less light is spread over the same area; the image gets dimmer. We would have to expose for longer to get the same amount of light in a given area. Therefore, large values of \(f\) imply slow telescopes, and vice-versa.

---

Refractors

The refracting telescope was the first type of telescope to be developed. The question of who invented the telescope is a controversial one. It is usually credited to the Dutch optician Hans Lippershey in 1608, although recent research suggests that a form of telescope may have been discovered by the Englishman Leonard Digges around 1550. The first person to systematically use a telescope for astronomy was the Italian scientist Galileo Galilei in 1610, however others were close behind, and the Englishman Thomas Harriot was the first to record a telescopic observation of the Moon, and Sunspots.

The refractor focuses light using a lens, known as the objective. The objective is usually made of glass and, in it's simplest form, has a bi-convex shape where both surfaces are sections of a sphere. The lens collects the parallel light from an astronomical source and forms an image of it, as shown in figure 35. This figure also shows that a simple refractor has a major defect, known as chromatic aberration. This aberration is the largest imperfection to affect astronomical telescopes.

Achromats and Apochromats

In 1758, the English optician John Dolland patented the achromatic doublet (or achromat). The achromat corrects for chromatic aberration by using two lenses made of different materials, typically crown and flint glass. The positive crown-glass lens strongly converges the light, but introduces strong chromatic aberration. The flint glass element is negative. It has a weak refractive index, so it does not undo the convergent effect of the crown glass element. However, the refractive index of flint glass changes rapidly with wavelength, and so it has a stronger effect on the blue light, thus correcting chromatic aberration. The situation is shown schematically in figure 37.

An achromatic doublet can only make the focus the same for two wavelengths and there is residual chromatic aberration at intermediate wavelengths. Nevertheless, achromats deliver order-of-magnitude reductions in chromatic aberration. Further improvement is possible by adding a third lens. These are called apochromats, and they can bring three wavelengths (e.g. red, green and blue) to the same focus. Even greater improvements can be obtained by adding more lenses, so-called super-apochromats, but these become economically unviable for the large apertures required for telescope objectives.

Refractors: Pros & Cons

Since apochromats use flint glass to undo some of the convergent effects of the crown glass element, one implication of using achromats to minimise aberrations is that the focal length becomes quite long. This makes refractors slow, with focal ratios around 10 to 20. The plate scale is therefore quite small, which spreads the image of a point source over a large area in the focal plane. This makes refractors a poor choice for faint objects, but ideal for planetary observations and astrometry (i.e. measuring the positions of stars).

One of the biggest issues with refractors is their practicality as we move to larger telescopes. The lens in a refractor has to be held by its edge, and as the lens becomes larger it starts sagging under its own weight and hence distorts the image; second, as the diameter of the lens increases, so does its thickness and thus so does the amount of light absorbed in the glass. As a result, the largest refractor currently in existence is the 40-inch (1m) telescope at Yerkes Observatory near Chicago, built in 1897. Figure 38 shows the immense scale of the telescope tube and dome - it is unlikely that a bigger refractor will ever be built.

Because of the immense challenge in building large refractors, most professional telescopes are reflecting telescopes.