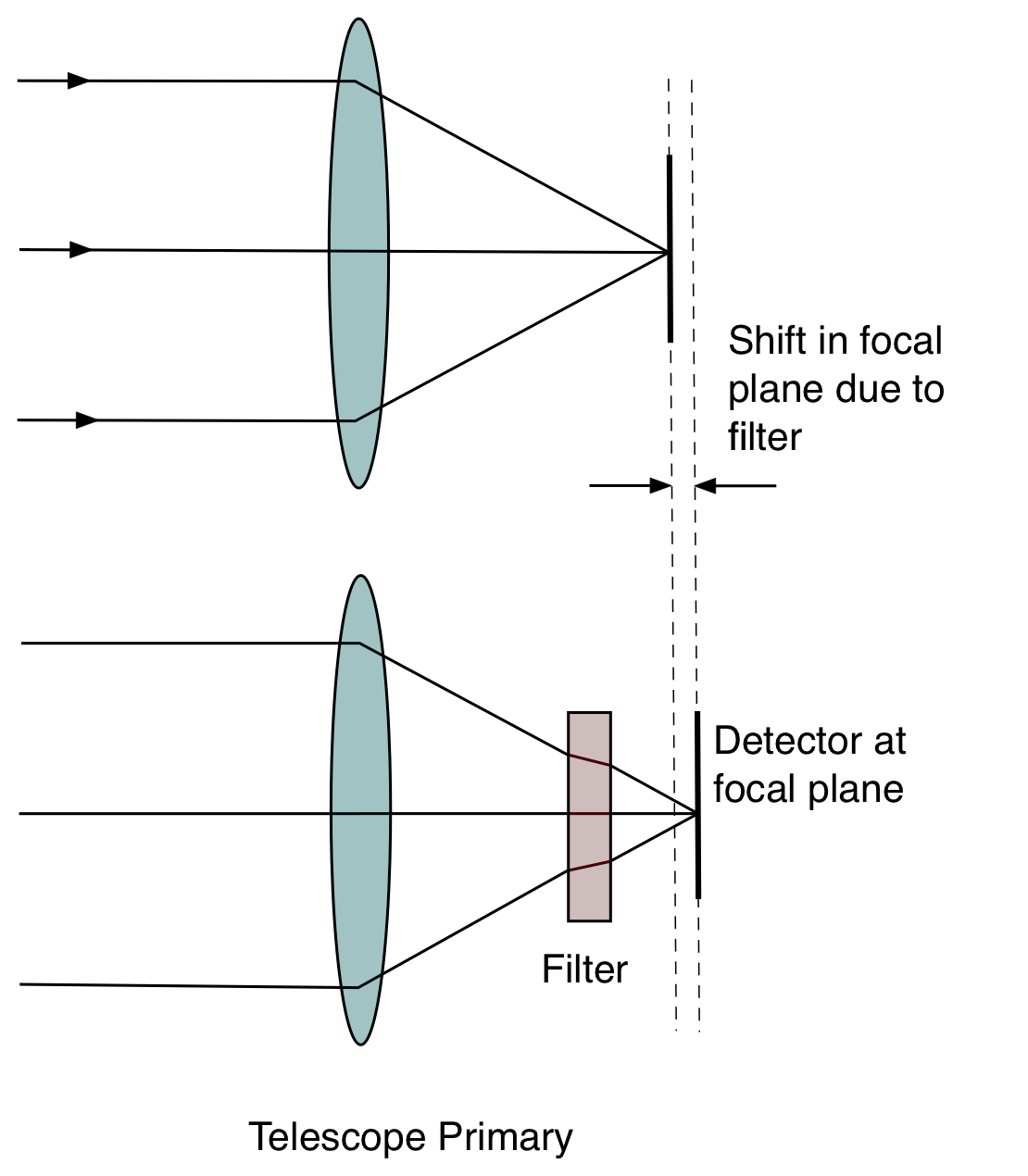
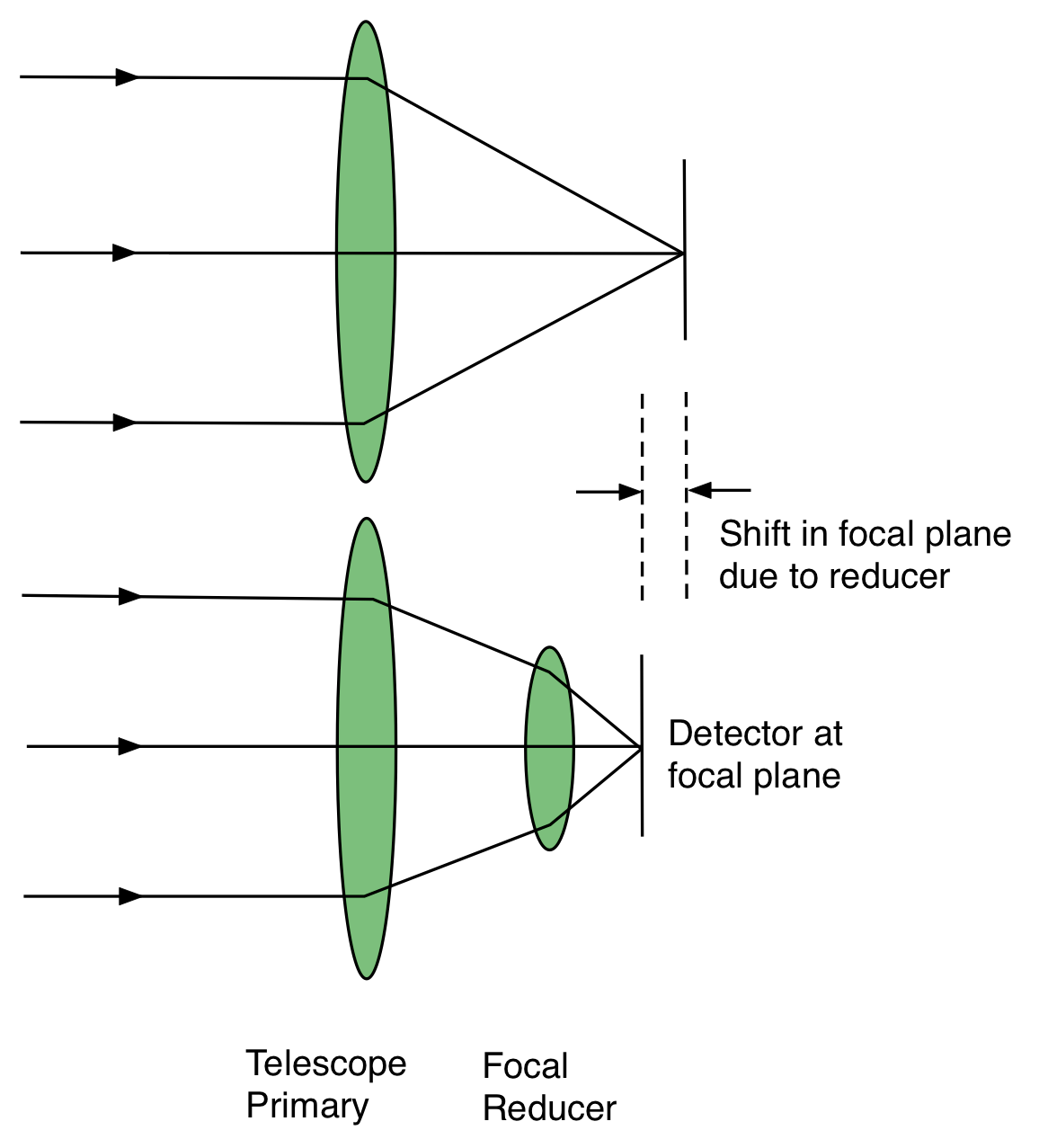
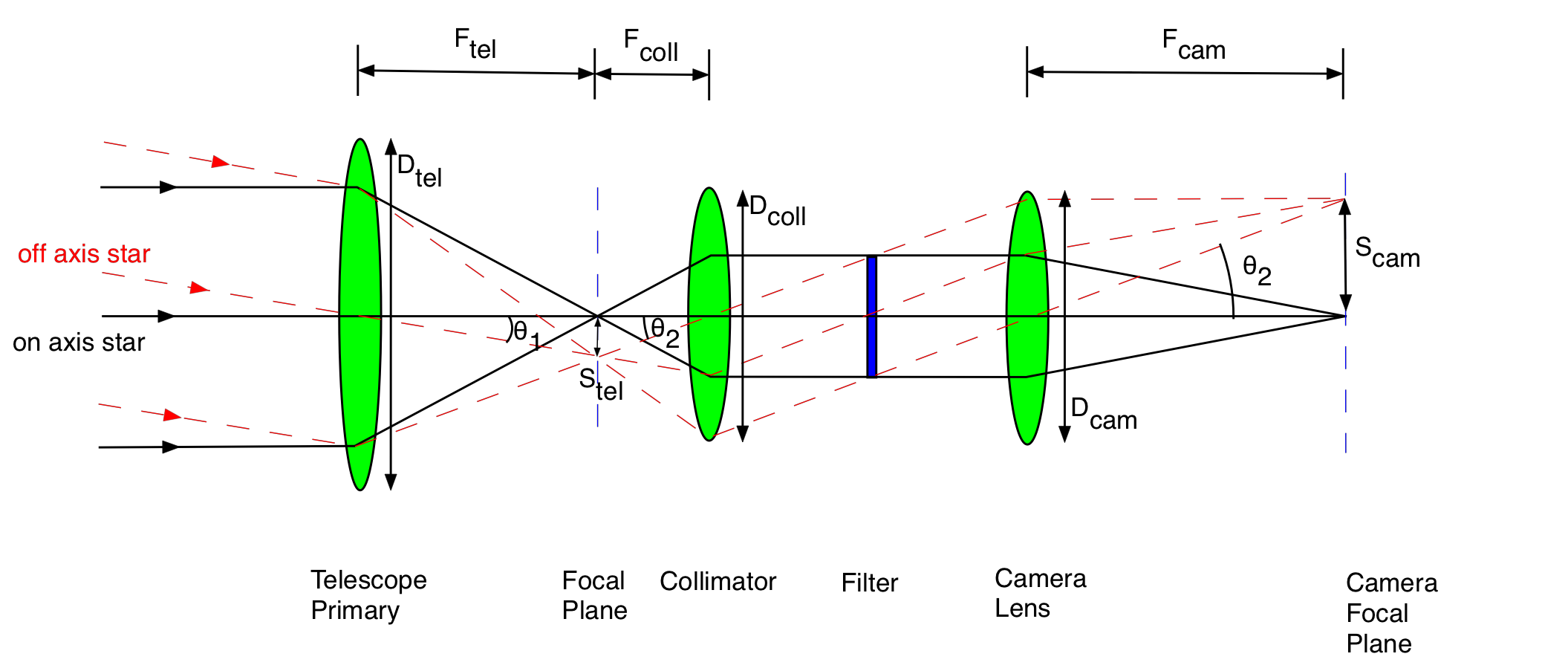
Focal Reducers/Enlargers
The issue with simple imagers is that they rely on the native plate scale. This may be wholly unsuitable. For
example a telescope with a focal length of 40m (say a 4m \(f/10\) Cassegrain) will have a plate
scale of 5 arcseconds/mm. Typical CCDs are 2000 pixels across, and each pixel is 13 \(\mu\)m, so
the total size of a CCD is around 25mm. The FoV of a simple imager would be around 2 arcminutes,
which is no use for wide-field use. In addition, each pixel would only be 0.06". If the seeing
was 1", we would have roughly 17 pixels across the seeing disc. Such a setup is non-optimal.
Optimal CCD Sampling
How many pixels should there be in the seeing disc? In the example above, we were spreading the
light out over a disc of diameter 17 pixels. Each pixel has read noise, so this means lots of read noise for
every star! On the other hand, if the pixels were larger than the seeing disc, the size of our
stars would be set by our pixel size, and not the seeing - we are throwing away spatial
resolution. As a compromise, it is common for instruments to be built so that the typical seeing
disc is sampled by two pixels. But how do we achieve that? Replacing the telescope for one of a
shorterfocal length, or the detector for one with more and/or larger pixels, is usually neither
apractical nor economical solution, so what can be done?