Understanding statistical inference is one of the most important skills an astronomer can develop. Moreover, it is one of the most important life skills you can possess; many political controversies or travesties of justice might be avoided if society at large had a better statistical literacy. Yet it tends to be something that undergraduate students avoid. In the next lecture, our aims are to equip you with the basic statistical skills you need. Much of this first lecture should be revision of material you have already covered in your course. However, I hope the way it is treated here adds clarity.

There is substantial debate in the world of statistics about what probabilities actually mean. There are two possible interpretations, which assert that a probability reflects either:

• the frequency of occurrence of something (frequentism), or
• the degree of belief in something (Bayesian statistics).

To some degree it doesn't matter, as long as we can get the same result under either interpretation. In this lecture, we will take whichever view is most convenient. For those who are interested, there is a discussion of how the two approaches differ in the old notes for PHY21

A definition:

We define probability by imagining repeatedly taking some measurement, and looking to see if event \(A\) occurs. The probability \(P(A)\) of event \(A\) is just the fraction of times that \(A\) occurs. Closely connected is the idea of a random variable \(x\), where each time you measure it's value, you get a different answer. Repeated measurements of some physical quantity can be thought of as random variables. Often \(x\) is a continuous variable that can take any value. We define the probability density function \(p(x)\) so that \(p(x)dx\) is the probability that \(x\) is in the range \(x\) to \(x + dx\).

---

Calculus of probabilities

Suppose we have two events that could occur \(A\) and \(B\). For example, we might roll a dice and get either a 1 or a 6. The probability that either \(A\) or \(B\) occur is \[P(A \, {\rm or} \, B) = P(A) + P(B).\] If we roll two dice, what is the joint probability that we get both \(A\) and \(B\)? If the two events are exclusive - that is they can't both occur in one dice roll - then \[P(A,B) = P(A) \, P(B).\] However, these formulae do not work if the two events are not exclusive. For example, when drawing cards from a pack, we could draw a red card \((A)\) or we could draw an ace \((B)\). Of course, we can also draw the ace of diamonds! For these types of events: \begin{aligned} P(A,B) &= P(A|B) \, P(B) = P(B|A) \, P(A) \\ P(A \, {\rm or} \, B) &= P(A) + P(B) - P(A,B). \end{aligned} Where the notation \(P(A|B)\) means the probability that \(A\) occurs given that \(B\) occurs, often called the conditional probability. A graphical proof of the second formula is shown in figure 101. We can re-arrange the first formula to show that \[P(B|A) = \frac{P(A|B) \, P(B)}{P(A)},\] which is known as Bayes Theorem. It seems trivial, but we will see in the next lecture that it has profound consequences for how we interpret scientific data.

---

What does \(x = \mu \pm \sigma\) actually mean?

Physics students are constantly being nagged to provide error bars on their measurements. But what do the error bars actually mean? Unless the author explicitly tells you, it's impossible to be certain. An error bar is a short-hand way of expressing the probability distribution function of the measurement \(p(x)\). Usually, it is a shorthand for saying that \(p(x)\) is a Gaussian distribution with a mean of \(\mu\) and a standard deviation of \(\sigma\): \[p(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left[ \frac{-(x-\mu)^2}{2\sigma^2} \right]} .\] The easiest way of thinking about this is the Bayesian way (we'll hear more about Bayesian statistics in the next lecture). Under that world view, \(p(x)\) represents our confidence about various values of \(x\). When we quote an error bar, we are normally assuming that this knowledge is represented by the Gaussian distribution. This is not a bad assumption because it is very often true. For example, the Poisson distribution which governs counting objects tends towards a Gaussian distribution for large N. The keen student may also want to look up the Central Limit Theorem and it's counterpart, the Fuzzy Central Limit Theorem, which show that most random processes produce Gaussian distributions.

Since the Gaussian distribution underlies the true meaning of error bars, let us look at some of its properties.

The Gaussian probability distribution

The shape of the Gaussian probability distribution is shown in figure 102. Probably one of the most important properties of the Gaussian distribution is the fact that , if \(x\) is a Gaussian random variable with mean \(\mu\) and standard deviation \(\sigma\), there is a roughly 30% chance that a measurement of \(x\) will yield a value greater which is 1\(\sigma\) or more away from the mean. Since our error bars are shorthand for \(\sigma\), this can be an easy way of checking if our error estimates are correct - see figure 103.

Estimating \(\mu\) and \(\sigma\)

This is all well and good, but of no use whatsoever unless we know what values to give to \(\mu\) and \(\sigma\). In some cases it is easy. For example, if we count \(N\) electrons in a pixel, we know that these are governed by the Poisson distribution, which - for large \(N\) - looks like a Gaussian with \(\mu = N\) and \(\sigma = \sqrt N\). Sometimes we will know from a piece of equipment what uncertainty our measurements should have. In the absence of all of these pieces of information we have to use the data themselves to estimate \(\mu\) and \(\sigma\).

Suppose we have \(N\) measurements of the same Gaussian random variable \(x\). It is possible to show that the sample mean is the best estimate of the mean, i,e \[ \mu = \frac{1}{N} \sum_i^N x_i.\] Similarly, the best estimate of the variance \(\sigma^2\) is the sample variance \[ \sigma^2 = \frac{\sum_i^N (x_i - \mu)^2}{N-1}.\]

---

Combining and Transforming Random Variables

Suppose \(x\) is a Gaussian random variable, with mean \(\mu_x\) and uncertainty \(\sigma_x\) . For example, it could represent our degree of confidence in the flux of a star. What is the uncertainty on some transformation \(y = f(x)\)? A relevant example would be to calculate the error on a magnitude, given the error on a measured flux. 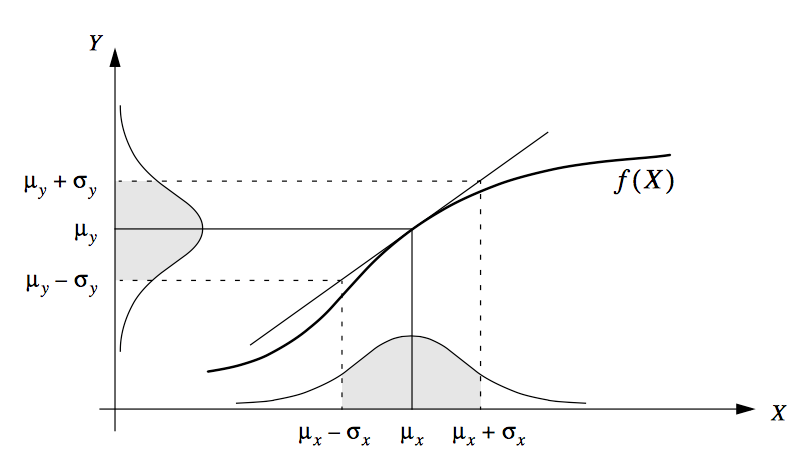We can approximate \(f(x)\) with a Taylor expansion around \(\mu_x\), \[f(x) \approx f(\mu_x) + \frac{df}{dx} \bigg|_{x=\mu_x} (x-\mu_x) + \ldots.\] This approximation is shown below in figure 104. Because \(f(\mu_x)\) and \( \frac{df}{dx} \big|_{x=\mu_x} \) are just numbers, under this approximation, \(y\) is also a Gaussian random variable, and we can calculate its mean and standard deviation to work out the uncertainty on \(y\).

The mean is straightforward, since \(\mu_y = f(\mu_x)\). To calculate the standard deviation, inspection of figure 104 shows that \[\mu_y + \sigma_y = f (\mu_x + \sigma_x).\] Using the Taylor expansion approximation we have \begin{align} \sigma_y &= f(\mu_x + \sigma_x) - \mu_y \\ &= f(\mu_x) + \frac{df}{dx} (\mu_x + \sigma_x - \mu_x) - \mu_y \\ &= \mu_y + \frac{df}{dx} \sigma_x - \mu_y \\ \sigma_y &= \frac{df}{dx} \sigma_x \end{align} It is vital to note that this is an approximation! You can see from figure 104 that if \(\sigma_x\) is large, the Taylor series becomes a poor approximation and the error bars will be incorrect. More seriously, \(y\) doesn't have a Gaussian PDF under a general transformation! A classic example of this is converting magnitudes to fluxes when the error is large.

Functions of multiple variables

We now look at the general case \(y = f(x_1,x_2,x_3,\ldots,x_n)\), where \(x_i\) is a Gaussian random variable. For example, \(x_i\) might be the number of counts in pixel \(i\), and we want to work out the error on the total number of counts from a star, \(y = \sum_i^N x_i\).

The formal derivation of the uncertainty on \(y\) is not straightforward, but we can get an idea by considering the contribution from each \(x_i\) in turn. From above, the uncertainty on \(y\) caused by uncertainty in \(x_i\) alone can be written \[\sigma_{y,i} = \frac{\partial f}{\partial x_i} \sigma_{x_i}.\] How are we to combine the contributions from each \(x_i\)? If we simply add them, a positive error may cancel with a negative error. This concept is obviously wrong - it's like saying that two uncertainties can somehow cancel and make an experiment more accurate. I hope it is intuitive that we should add the contributions in quadrature, e.g \[\sigma_y^2 = \left( \frac{\partial f}{\partial x_1} \right) ^2 \sigma_{x_1}^2 + \left( \frac{\partial f}{\partial x_2} \right) ^2 \sigma_{x_2}^2 + \ldots + \left( \frac{\partial f}{\partial x_n}\right) ^2 \sigma_{x_n} ^2= \sum_i^n \left( \frac{\partial f}{\partial x_i}\right) ^2 \sigma_{x_i}^2 \] This is known as the equation for error propagation.

Some worked examples

The equation for error propagation looks like a nightmare. However, it is not as bad as it looks. Let us look at a few familiar examples to show that it produces the results we expect, before moving on to examples more relevant to astronomy.

Sums of two variables

Suppose we measure \(x\) and \(y\), each with uncertainties \(\sigma_x\) and \(\sigma_y\). Whats the uncertainty in \(z = x + y\)? From the equation of error propagation \begin{align} \sigma_z^2 &= \left( \frac{\partial z}{\partial x} \right) ^2 \sigma_x^2 + \left( \frac{\partial z}{\partial y} \right) ^2 \sigma_y^2 \\ \sigma_z^2 &= \sigma_x^2 + \sigma_y^2, \end{align} as you might expect if you have covered error propagation using simple rules.

Sums of two variables

What is the uncertainty in \(z = xy\). Again, the equation of error propagation gives \begin{align} \sigma_z^2 &= \left( \frac{\partial z}{\partial x} \right) ^2 \sigma_x^2 + \left( \frac{\partial z}{\partial y} \right) ^2 \sigma_y^2 \\ \sigma_z^2 &= y^2 \sigma_x^2 + x^2 \sigma_y^2, \\ \end{align} which we divide by \(z^2 = x^2y^2\) to get \[ \left( \frac{\sigma_z}{z} \right) ^2 = \left( \frac{\sigma_x}{x} \right) ^2 + \left( \frac{\sigma_y}{y}\right) ^2,\] again, as we expect.

Error on the mean

Suppose we obtain \(N\) measurements of a single value \(x_i\), each with an uncertainty of \(\sigma_x\). We calculate the mean \(z = \sum_i^N x_i / N\). What is the error on the mean? Since \(z = \frac{x_1}{N} + \frac{x_2}{N} + \ldots + \frac{x_N}{N}\), then \[ \frac{\partial z}{\partial x_i} = \frac{1}{N} .\] Therefore, the error propagation equation gives \[ \sigma_z^2 = \sum_i^N \frac{1}{N^2} \sigma_x^2 = \frac{N}{N^2} \sigma_x^2 = \frac{\sigma_x^2}{N},\] which can be re-written \[\sigma_z = \sigma_x / \sqrt{N}.\]

Looking at the examples above, you can see that the equation of error propagation can be used to derive all the error rules you may have learned previously. It is more useful to remember the equation than these rules, since it can be applied to any combination of random variables. We will illustrate this shortly. but first I want to show an example of how we might use errors in practice.

Comparing measured experimental results

This is a particularly important example, because it is related to comparing two measurements of the same quantity, as measured by experiment. Suppose experiment \(A\) measures Hubble's constant to be \(H_0 = 63.4 \pm 0.5\) km/s/Mpc, but experiment \(B\) measures it to be \(H_0 = 73.5 \pm 1.4\) km/s/Mpc. Do they disagree? Well, there are two options: either the experiments are finding different values for \(H_0\), or they are actually measuring the same value, and the reported numbers disagree purely because they are random variables, and so move around a bit by chance.

Well, we can calculate the difference \(\Delta\) between the two measurements \(\Delta = B-A = 10.1\) km/s/Mpc. We can also calculate the uncertainty \( \sigma_{\Delta} = \sqrt{\sigma_A^2 + \sigma_B^2} = 1.5 \). We can write that \( \Delta = 10.1 \pm 1.5 \) km/s/Mpc. But recall that this is shorthand for saying that our confidence in the true value of \(\Delta\) is represented by a Gaussian of mean 10.1 and a standard deviation of 1.5. 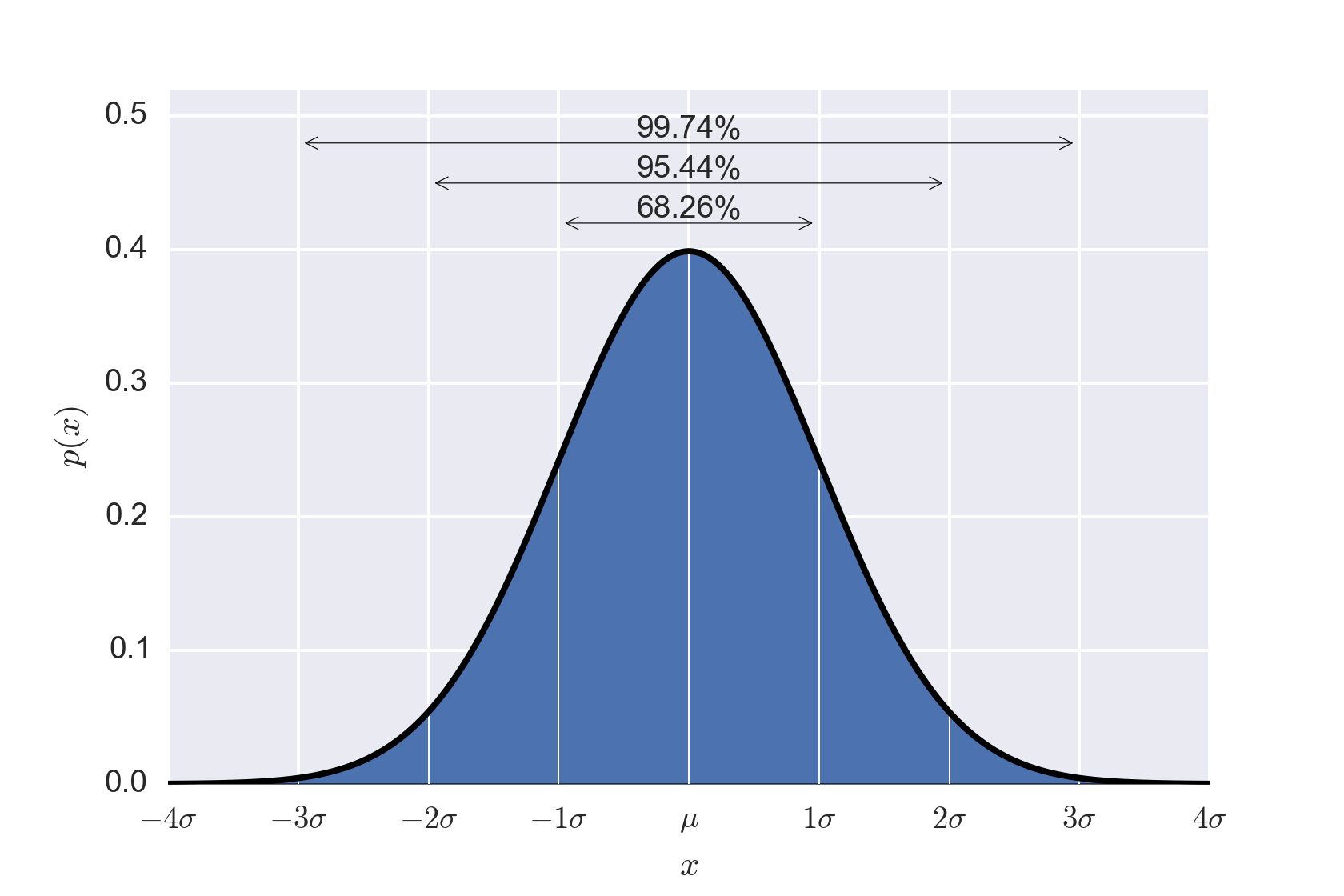The mean of this Gaussian is 6.7 standard deviations away from zero - which is the value we'd expect if there was no disagreement. As seen in figure 102, values 6.7 standard deviations from the mean are highly unlikely to happen by chance. We therefore conclude the values disagree

---

Errors on Magnitudes

To begin with, we assume that the errors on the magnitudes are small. Otherwise, the approximation we made in figure 104 is not valid and we cannot apply the equation of error propagation. The magnitude equation is \(m = -2.5 \log_{10} f + c\). Therefore \[\sigma_m = \frac{dm}{df} \sigma_f.\] To differentiate \(\log_{10} f\) we use the change of base formula to write \[ \log_{10} f = \frac{ \ln f }{\ln 10} \approx \frac{\ln f}{2.3} .\] Therefore, \(m = -\frac{2.5}{2.3} \ln f + c\) and \[ \frac{dm}{df} \approx \frac{-2.5}{2.3f} = \frac{1.09}{f},\] and \[ | \sigma_m | = 1.09 \frac{ \sigma_f }{ f} \approx \frac{ \sigma_f }{ f},\] where we have ignored the sign of \(\sigma_m\). Thus, to a rough approximation (and for small errors), the uncertainty in the magnitude is equal to the fractional error on the flux.

For example, suppose we measure the magnitude of a star as \(m = 15 \pm 0.1\). This means that \(\sigma_f = 0.1 f\) - the flux is measured with an uncertainty of 10%. Put another way, the signal-to-noise ratio of this measurement is \(\frac{f}{\sigma_f} = 10\). Remembering this approximation is an excellent way to quickly understand the precision of astronomical brightness measurements. A magnitude error of 0.1 corresponds to a signal/noise ratio of 10. A magnitude error of 0.01 corresponds to a signal to noise ratio of 100, or a measure of the flux with 1% uncertainty.