L19: The Bayesian Astronomer

L19: The Bayesian Astronomer a clearer way to think about stats

Introduction

We now know enough about error bars and uncertainties to be able to calculate them for our data points. This is half the battle. In this lecture we will show how those uncertainties are used to test scientific hypotheses and models. In doing so we will discuss Bayesian statistics; an approach which is in my view more intuitive and useful than the frequentist view discussed in the previous lecture.

The Likelihood function

Frequentists use a property known as the Likelihood to test models and hypotheses. The Likelihood is the probability that we would obtain our data \(D\), given a model \(M\) or a hypothesis \(H\). It is written \(L \equiv P(D \mid M) \) or \(L \equiv P(D \mid H) \). In plain English, the Likelihood is the probability of the data, given the model. In the first half of this lecture we will show how to use the Likelihood to test hypotheses and fit models.

In the second half of the lecture we will introduce a world of statistical controversy, and introduce Bayesian statistics.

Hypothesis Testing

A common problem in science is to ask whether our data is consistent with some hypothesis, \(H\). For example, I have a hypothesis that the flux of a star is \(S\). Let's say I observe the star - how do I use my data to test this hypothesis?

Suppose that the hypothesis \(H\) is correct; in my exposure I would expect to detect \(N=400\) electrons. Therefore given this hypothesis if I took many of these exposures the number of electrons in each would follow a Poisson distribution, well approximated by a Gaussian distribution with \(\mu = 400\) and \(\sigma = 20\).

Suppose I actually take an exposure, and detect 385 electrons. What is the chance that we would have detected this many electrons or fewer, if we assume the original hypothesis is correct. Our measurement is 0.75\(\sigma\) from the mean, and the Gaussian PDF implies that we expect this to occur 22% of the time. This is the Likelihood of getting our data (385 electrons or less), given our hypothesis. This is not very unlikely, so I see no reason to assume our original hypothesis is incorrect.

This is the way a frequentist tests a hypothesis. They assume the hypothesis is true (the null hypothesis), and ask how likely their data is to occur, given the hypothesis. This probability is called the p-value. Typically, scientists will conclude there is reason to reject the null hypothesis if \(p < 0.05\). We will see later how this can lead to trouble.

Some useful statistical tests

Don't worry about trying to revise this section. It is here for your reference later in the course. In it I outline a few tests which use the above technique, and when you might consider using them.

Spearman Rank Correlation

The null hypothesis is that two variables \(x\) and \(y\) are not correlated. This test will return a statistic which tends towards +1 for perfect linear correlation, and -1 for perfect linear anti-correlation. For a given correlation coefficient \(r\), a \(p\)-value can be calculated by randomly shuffling your data many times, and seeing how many times the shuffled data gives a correlation coefficient of size greater than or equal to \(r\).

Students-t test

Actually a whole family of tests. The most common example is comparing two samples to see if they have the same true mean. The name derives from the fact that, under the null hypothesis that the two samples share a true mean, the difference between the sample means follows a mathematical distribution known as the t-distribution

Kolmogorov-Smirnov (KS) test

A very useful test to see if two samples were drawn from the same distribution. The null hypothesis is that both distributions are the same. For example, we might have measured the masses of stars in two star clusters, and wish to test if they are drawn from the same mass distribution.

Model Fitting

Probably the most common task for an observational astronomer is fitting a model to some data. Model fitting can be thought of as an extension of hypothesis testing. Suppose we have a model \(M\) with some parameters \(\theta\). For example, our model, \(M\) could be a straight line \(y = mx+c\), with parameters \(\theta = (m,c)\). Model fitting is the process of finding the parameters which best fit our data, and the corresponding uncertainties on them. To do this, we obviously have to have some measure of how well our model fits our data.

The \(\chi^2\) statistic

This is the most commonly used measure of goodness-of-fit. Suppose we have a model \(y(x)\) and we observe a set of points \((x_i,y_i)\), each with corresponding uncertainties \(\sigma_i\). The \(\chi^2\) statistic is \[\chi^2 = \sum_i \left(\frac{y_i - y(x_i)}{\sigma_i} \right) ^2,\] where \(y(x_i)\) is the prediction of our model at \(x_i\). Intuitively, we can see that \(\chi^2\) measures goodness of fit. The quantity \( [y_i - y(x_i)]/\sigma_i \) is a measure of how many error bars a data point is away from our model. We saw in a previous lecture that if our model fits well, most data points lie within 1\(\sigma\), but a third lie further away. Therefore, we'd expect \(\chi^2\) for a good fit to roughly equal the number of data points. Poor fits will yield larger versions of \(\chi^2\). A common way to fit a model is therefore to find the model parameters which minimise \(\chi^2\).

How to use a computer to automatically find the model parameters which give the lowest \(\chi^2\) is a whole other lecture course! Suffice it to say that several different algorithms exist, which you can usually find in libraries for your computer language of choice; either the numerical recipes library for C/C++ (the University Library and Astro Library have copies) or scipy for Python. Some of these algorithms will also give uncertainties on the model parameters - these are usually calculated by seeing how much the model parameters can change before \(\chi^2\) increases too much.

Justifying \(\chi^2\) - The principle of maximum likelihood

Here we will show why minimising \(\chi^2\) is a sensible way of fitting a model to data. We will show that minimising \(\chi^2\) is equivalent to maximising the Likelihood - the probability of obtaining our data, assuming our model is correct.

We start by assuming our model is true. We then know the predicted value of \(y(x)\). If measurement \(i\) has an error \(\sigma_i\) then our \(i^{\rm th}\) data point is a Gaussian random variable with mean \(\mu = y(x)\) and standard deviation \(\sigma_i\). The probability that this datapoint has the value it does (\(y_i\)) is therefore given by \[P(y_i \mid \theta) = \frac{1}{\sqrt{2\pi\sigma_i^2}} \exp{ \left[ \frac{-(y_i - y(x_i))^2 }{2\sigma_i^2} \right] }.\] We assume the data points are independent, so the Likelihood, or the probability of getting our whole dataset is \begin{align} P(y_1,y_2,\ldots,y_n \mid \theta) &= P(y_1 \mid \theta) P(y_2 \mid \theta) \ldots P(y_n \mid \theta) \\ &= \prod_{i=1}^n P(y_i \mid \theta) \\ &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma_i^2}} \exp{ \left[ \frac{-(y_i - y(x_i))^2 }{2\sigma_i^2} \right] } \\ &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma_i^2}} \prod_{i=1}^n \exp{ \left[ \frac{-(y_i - y(x_i))^2 }{2\sigma_i^2} \right] } \\ L = P(D \mid \theta) &= \alpha \prod_{i=1}^n \exp{ \left[ \frac{-(y_i - y(x_i))^2 }{2\sigma_i^2} \right]}, \end{align} where \(\alpha\) is a constant. We now take the natural log of the Likelihood to obtain \[ \ln L = \ln \alpha - \frac{1}{2} \sum_{i=1}^n \left(\frac{y_i - y(x_i)}{\sigma_i} \right) ^2.\] But the sum on the RHS is just \(\chi^2\), so we can write \[ \ln L \propto -\chi^2.\] Therefore the model parameters which minimise \(\chi^2\) will maximise the Likelihood - the probability of obtaining our data, assuming our model.

Beyond Frequentism: Bayesian Statistics

**Figure 107:** a cartoon Venn diagram depicting the issue many Bayesian statisticians have with frequentist thinking.

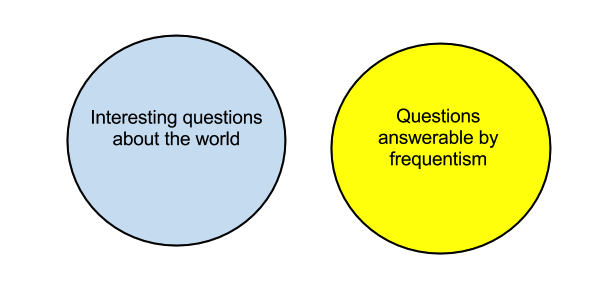
A frequentist asks "given my hypothesis, how likely is my data" - they calculate \(P(D \mid H)\). Much of the criticism of frequentism arises from the fact that most of the time this is the wrong question to ask. We really want to know is \(P(H \mid D)\) - how likely the hypothesis is, given the data! Unfortunately many scientists don't understand this subtlety. The result is that confusion arises, and scientists publishing in Nature are surprised to find 20% of published results based on P-values smaller than 0.05 are probably wrong.

Remember - a P-value is the chance of getting my data, assuming my hypothesis is true. When testing a drug, we may start with the hypothesis that the drug does not work. A small P-value means the data was unlikely to arise given the hypothesis. It is tempting to conclude that the hypothesis was wrong, and the drug does work.

We will see that this is a serious mistake, which arises as a failure to compare the small Likelihood of my data to the probability that my hypothesis is true in the first place. I illustrate the problem with a common thought experiment.

Bayes Theorem and Medical Tests

Suppose I am worried about my health and fear I have Rabies. I go for a test. My null hypothesis is that I do not have Rabies. The test is positive. The Likelihood that the test is positive, given that I do not have Rabies is 1%. What is the chance I have Rabies after all?

If you answered 99% you have fallen foul of the 'base rate fallacy', also known as the 'prosecutors fallacy'. To answer the question correctly, let's imagine testing the whole population of Sheffield, 60 000 people. Let's say we know that, on average, 0.1% of people have Rabies at any time. Prior to taking the test, this is my best guess for the chance that I have the disease. We say the prior probability of having Rabies is 0.1%. In Sheffield then, at any one time 60 people have Rabies, and 59 940 people do not. When we test the whole population, 1% of these 59 940 people will receive a positive test. Thats 599 people who falsely test positive. If all the people who do have Rabies also test positive, that's 659 positive tests in total.

Let us ask this question - given I have had a positive test, what are the chances I have Rabies? Well, out of all 659 positive tests, 60 of them are genuinely sick people. Therefore the conditional probability that I have Rabies, given a positive test is \(60 / 659 \approx 9\)%. I am much more likely to be well than not - even after a positive test!

The confusion arises because although the Likelihood of a positive test was small, we were testing a hypothesis which was itself very unlikely. This is why it is so important to compare the Likelihood with the prior probability of your null hypothesis. It is why tests using the Likelihood can be so misleading. It is for this reason that particle physicists required such a high threshold (5\(\sigma\)) for claiming the detection of the Higgs boson. It is also the reason why so many scientific studies with apparently significant p-values are wrong - the claims they were making were very unlikely, and so needed extra-ordinary levels of evidence. As well as it's impact in science, ignorance of the base rate fallacy has widespread ramifications in society. People have spent years in jail due to a failure to understand this point. We shall now look at how to fix this problem using Bayes theorem.

Recall Bayes Theorem states that \[P(B \mid A) = \frac{P(A \mid B) \, P(B)}{P(A)}.\] Let's label the event that I have Rabies as \(R\), and the event of a positive test \(T^+\). Bayes Theorem tells us that the probability I have Rabies, given my positive test is \[P(R \mid T^+) = \frac{P( T^+ \mid R) \, P(R)}{P(T^+)}.\] We assume the test always works when someone does have Rabies, i.e \(P( T^+ \mid R) = 1\). We know the prior probability that I have Rabies is 1%, i.e \(P(R) = 0.001\). What is \(P(T^+)\)? Well, I either have Rabies (event \(R\)) or I do not (event \(\tilde{R}\)). I can get a positive test in either case, so the probability I receive a positive test is \[P(T^+) = P( T^+ \mid R) \, P(R) + P( T^+ \mid \tilde{R}) \, P(\tilde{R}) = 1 \times 0.001 + 0.01 \times 0.999 = 0.01099.\] Putting this all together gives the correct chance that I have Rabies given a positive test, \(P(R \mid T^+) = 0.09\). Phew.

Bayesian Model Fitting

How does this relate to model fitting? The Bayesian approach to model fitting is to find the probability distribution of the model parameters, given the data, \(p (\theta \mid D)\). We use Bayes theorem to see how this relates to model fitting by minimising \(\chi^2\). Using Bayes theorem, we can write \[ p(\theta \mid D) = \frac{ p(\theta) \,p(D \mid \theta) }{ p(D) }.\] Let's examine the equation term by term.

\(p(\theta \mid D)\) is what we want to know. What is our knowledge of the model parameters given both our data, and our prior information? This is referred to as the posterior probability distribution.
\(p(\theta)\) is the prior, and represents the prior probability that the model parameters take a particular value.
\(p(D \mid \theta)\) is the Likelihood - how likely is our data given our model parameters and our prior knowledge?
\(p(D)\) is known as the evidence. It is the odds of getting our data given only our prior knowledge, regardless of the model parameters.

Very often the evidence is very hard to calculate. We can get round this by noting that it is a constant (i.e it doesn't depend on the model parameters), so we can write. \[ p(\theta \mid D) \propto p(\theta) \,p(D \mid \theta). \] We can work out the constant of proportionality by noting that \(\int_{\infty}^{\infty} p(\theta \mid D) d\theta = 1\).

Like \(\chi^2\) minimisation, many algorithms exist to perform Bayesian model fitting. The most widely used in astronomy is the Markov-Chain Monte-Carlo (MCMC) algorithm. A great Python library for fitting a model to data using MCMC is emcee. These algorithms will estimate the full posterior probability distributions for your model parameters, from which you can calculate both the mean (best fit) and standard deviation (error bars).

When to use Bayesian Model Fitting

Here is a good question. When should you fit a model with \(\chi^2\) minimisation, and when should you use a Bayesian method? Remember we can write Bayes theorem as \( p(\theta \mid D) \propto p(\theta) \,p(D \mid \theta). \) Therefore, if \(p(\theta) = \mathrm{const}\), we have \( p(\theta \mid D) \propto p(D \mid \theta) = L\). In other words, if you suspect your prior distributions are flat - independent of the parameter values - then Bayesian fitting and \(\chi^2\) minimisation are identical.

Choosing distributions for the priors can sometimes be hard. It is always subjective. The need to choose a prior is one of the most common criticisms of Bayesian methods, however we can see above that choosing to minimise \(\chi^2\) is also choosing a prior - a flat one in this case. Priors can reflect physical certainty - i.e I know a speed must lie between 0 and \(c\). They can reflect previous measurements of a model parameter - i.e if my model has Hubble's constant as a parameter, we have good prior knowledge that \(H_0 = 69.6 \pm 0.7\) km/s/Mpc. Thus I would probably choose to represent \(P(H_0)\) as a Gaussian with mean 69.6 and standard deviation of 0.7 km/s/Mpc.

An astronomical application of Bayes theorem: distance estimation

Suppose we measure the parallax to a star, and find it's parallax is \(\pi = (6.6 \pm 1.1) \times 10^{-3}\) arcseconds. What is the most likely distance to the star? This seems simple, but we have to remember the prior. A star is a-priori more likely to lie at a large distance, since a large spherical shell has a larger volume than a small one.

The probability of a distance \(d\) given our observation \(O\) is \[ P(d \mid O) \propto P(d) \, P(O | d), \] where \(P(d)\) is the prior probability of a given distance. Now the Likelihood of our parallax observation \(O\), given a distance is a Gaussian with some mean and standard deviation. The mean can be found from \(\bar{d} = f(\pi) = 1/\pi = 150\) pc. We can find the standard deviation by applying the error propagation formula to find \(\sigma_d = \sigma_{\pi} / \pi^2 = 30\) pc. Therefore \(P(O \mid d)\) is a Gaussian with a mean of 150 and a standard deviation of 30, as shown in figure 108.

What about the prior? Well, the probability of a star lying in a spherical shell with radius \(r\) and thickness \(dr\) is proportional to the volume of that shell \(4\pi r^2 dr\). The probability that the distance is between \(r\) and \(r+dr\) is therefore \(P(r)dr \propto r^2 dr\). Therefore we have \(P(r) \propto r^2\). Putting all this together we have \[ P(d \mid O) \propto P(d) \, P(O | d) \propto d^2 \exp{\left( \frac{-(d-150)^2}{2\times30^2} \right) }. \] This probability distribution is also plotted in figure 108. You can see the bias towards large distances that we would have missed had we not taken a Bayesian approach.

Figure 108: Bayesian distance estimation. The measured parallax naively suggests a distance of \(150 \pm 30\) pc. This is shown in the histogram, and the green line. Proper consideration of the prior knowledge of the distance gives the probability distribution in red, which is biased towards larger distances, and has a most probable distance of 161 pc.