Introduction

No astronomical measurement is without noise. This noise limits the precision of any measurement made from our data. As a result, probably the most important skill for the practical astronomer is to be able to estimate the noise in their planned observations, and determine if the observations will meet their requirements. In this lecture, we learn how to calculate the noise levels in an astronomical observation.

Photon Statistics

No astronomical measurement is without noise. This noise limits the precision of any measurement made from our data. As a result, probably the most important skill for the practical astronomer is to be able to estimate the noise in their planned observations, and determine if the observations will meet their requirements. In this lecture, we learn how to calculate the noise levels in an astronomical observation.

The vast majority of astronomical sources emit photons at random. Therefore, when these photons reach our telescope, they are randomly spaced. Consider the situation shown in figure 56. On average, this source is emitting 4 photons per second, but they are randomly spaced. Therefore, in any given 1s exposure, we will not detect exactly 4 photons. Suppose we turn the problem around, and in a 1s exposure we detect 7 photons (as we do in the time interval t=1-2s in figure 56 above). This does not mean the source emits 7 photons/sec on average. This random bunching of photons introduces noise into our measurements of stellar flux. This variation is known as shot noise. It represents the irreducible minimum level of noise present in an astronomical observation.

If the number of photons received in a fixed interval of time has an average value \(N\), but the photons are randomly spaced, the probability of detecting \(k\) photons in the fixed time interval is given by the Poisson distribution, \[P(k) = \frac{N^k e^{-N}}{k!}.\] In astronomy, we are often dealing with large \(N\), and for large N (i.e \(N \gtrsim 5\)) the Poisson distribution tends towards our old favourite, the Gaussian distribution, with a mean of \(N\), and a standard deviation of \(\sigma = \sqrt{N}\), \[P(k) = \frac{1}{ \sqrt{2\pi\sigma^2} } e^{-(k-N)^2/2\sigma^2}.\] Therefore, if we detect \(N\) photons per second from an astronomical source, the best we can do is to say that the true mean photon rate from the star has a likely mean of \(N\), and an uncertainty of \(\sqrt{N}\). However, it is vital to note that this conclusion does not just apply to photons from stars, but to any process when we are counting random events which occur at an average rate. For example, it applies equally to the counting of photons from the sky (i.e sky background), or the production of thermally-generated electrons in a semi-conductor (i.e. dark current).

For a perfect astronomical detector in space, this shot noise would set a limit on the accuracy with which we could measure the photon rate. We would say the noise on the measurement would be \(\sqrt{N}\).

---

Signal-to-Noise Ratio

A crucial quantity for astronomical observations is the ratio of the signal from an astronomical source, \(S\), to the noise, \(N\). The signal-to-noise ratio, is given by \[{\rm SNR} = S/N.\] For example, if we measure 100 photons from a star (\(S\)), the shot noise (\(N\)) is 10 photons and we would have a SNR=10. We might also say the noise is one tenth of the signal, or that the error bar on the flux is 10% of the total flux. The SNR thus sets the accuracy with which the flux can be measured.

The "signal" part of the signal-to-noise ratio doesn't always refer to the flux of the star. For example, if we were trying to measure the variability of a star, the "signal" part could refer to the amplitude of variability. Suppose, for example, the variability of the star is 20% of the mean flux. If the noise in our flux measurements is 4% of the mean flux, then the variability is measured with a signal-to-noise ratio given by \[ {\rm SNR} = 20/4 = 5.\] This is shown in figure 57.

---

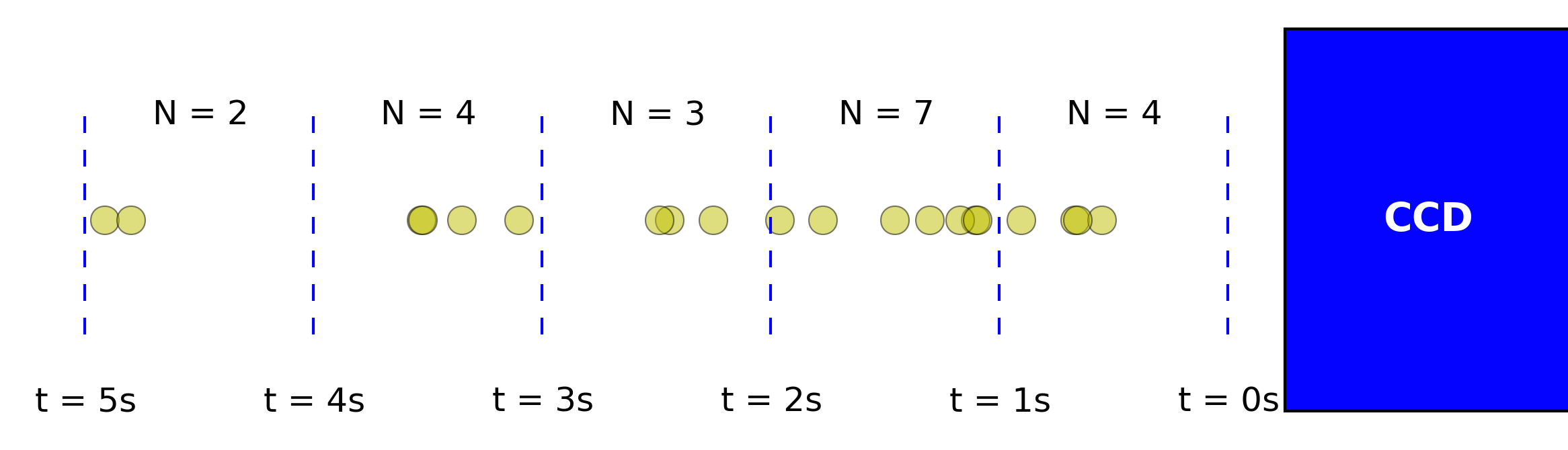
The CCD Signal-to-Noise Equation

For CCD observations there are several sources of noise. Suppose the number of photo-electrons detected from the object, sky background and dark current are \(S_o, S_s\) and \(S_d\), respectively. Then the various noise sources, and their amplitudes (standard deviations) are:

• shot-noise in the detected photo-electrons from the source, \(\sqrt{S_o}\);
• shot-noise in the detected photo-electrons from the sky background, \(\sqrt{S_s}\);
• shot-noise in the thermally excited electrons, i.e the dark current, \(\sqrt{S_d}\);
• time-independent readout noise, \(R\). Note there is no square root here. The readout noise is the standard deviation in the number of electrons measure - it is not a Poissonian counting process.

It is extremely important to realise that these noise sources are present even after the mean sky background or dark current has been subtracted. The measured value of any CCD pixel differs from it's true value by some unknown amount due to noise. The values above tell us the typical size of this unknown noise, but not it's exact value. Subtracting the sky during photometry, or subtracting dark frames does not remove the shot noise from the CCD pixels!

We can assume all the noise sources are independent. When we add Gaussian random variables, the variance \(\sigma_T^2\) of the result is equal to the sum of the variances of each Gaussian, \(\sigma^2_T = \Sigma_i^n \sigma^2_i\) . The total noise, \(N\), is equal to the standard deviation \(\sigma_T\), and is therefore given by: \[N = \sqrt{S_o + S_s + S_d + R^2}.\] Hence, the SNR is given by \[{\rm SNR} = S_o/N = \frac{S_o}{\sqrt{S_o + S_s + S_d + R^2}}.\]

CCD equation in units of counts (ADU)

Typically, when predicting the SNR of a CCD observation we have the following quantities to hand:

• \(S_o\), in units of photons per second;
• \(S_s\), in units of photons per second per pixel;
• \(S_d\), in units of electrons per second per pixel;
• \(R\), in units of electrons per pixel.

A few things are worthy of comment in the above list. First, \(S_o\) is the total number of photons from the object, which will probably be spread out over a number of pixels, whereas \(S_s\) is the number of sky photons per pixel. Second, \(S_o\) and \(S_s\) are in photon units not electrons. Third, \(S_o\), \(S_s\) and \(S_d\) will increase with exposure time, but \(R\) will not.

We need to use electrons in the SNR equation above, not the number of photons emitted by the source. Poissonian statistics apply to whatever we are counting, and in this case we are counting electrons! The total number of electrons detected from the source is given by \[S_o Qt,\] where \(t\) is the exposure time in seconds, and \(Q\) is the Quantum efficiency of the CCD, expressed as a number between 0 and 1. Similarly, the total number of electrons detected from the sky is \[S_s Qt n_p,\] where \(n_p\) is the number of pixels that the object is spread over. Using similar arguments for the other terms, the CCD SNR equation is written as \[{\rm SNR} = \frac{S_o Qt}{ \sqrt{ S_o Qt + S_s Qt n_p + S_d t n_p + R^2 n_p } }.\]

Sometimes \(S_o\) and \(S_s\) will be in different units - astronomers do like to be awkward, after all. We always need to convert them to units of electrons, as electrons are the thing that's actually being counted, and thus obeys Poissonian statistics. With \(S_o\) and \(S_s\) in photons, we converted to electrons using the QE. If \(S_o\) and \(S_s\) are given in counts, we convert from counts to electrons by using the CCD gain \(G\) in place of the QE \(Q\). The SNR CCD equation becomes \[{\rm SNR} = \frac{S_o Gt}{ \sqrt{ S_o Gt + S_s Gt n_p + S_d t n_p + R^2 n_p } }.\] Finally, one might also find \(S_o\) and \(S_s\) given in flux units. In that case we divide the flux by the average energy of a single photon in this bandpass to find the number of photons arriving per second, and then use the QE \(Q\) to convert to electrons per second.

Limiting Cases

There are three limiting cases for the CCD SNR equation. Using the simplified form \({\rm SNR} = S_o / \sqrt{S_o + S_d + S_s + R^2}\), we find that the these limiting cases are:

• Object Limited - \(S_o\) is much greater than \(S_s\), \(S_d\) and \(R^2\). In this case \[{\rm SNR} = S_o / \sqrt{S_o} = \sqrt{S_o}.\] Since \(S_o \propto t\), this means that \({\rm SNR} \propto \sqrt t\). In addition, \(S_o \propto D^2\), where \(D\) is the telescope aperture. Therefore \({\rm SNR} \propto D\).
• Background Limited - \(S_s\) is much greater than \(S_o\), \(S_d\) and \(R^2\). In this case \[{\rm SNR} = S_o / \sqrt{S_s}.\] In this case, since both \(S_s\) and \(S_o\) scale the same way with exposure time and telescope aperture, the SNR scales with respect to these values in the same way as the object limited case. For a fixed \(S_o\), the SNR scales with the square root of the sky signal \(S_s\). It is therefore very important to observe faint sources when the sky is faint. Scattered light from the from the Moon is a major source of sky background, so faint sources should be observed near new Moon.
• Read Noise Limited - \(R^2\) is much greater than \(S_s\), \(S_o\) and \(S_d\). Since all these quantities scale with exposure time, but \(R\) does not, short exposures are often read noise limited. In this case \[{\rm SNR} = S_o / R.\] Since the readout noise is independent of integration time or telescope aperture, the SNR will now increase linearly with exposure time and as the square of the telescope aperture diameter.